Introduction and summary
Recent research on lesbian, gay, bisexual, and transgender (LGBT) people in the United States shows that they are more vulnerable to poverty than are heterosexual people with similar characteristics. Biased attitudes and discrimination might limit economic opportunities for LGBT people, so it is likely that low-wage jobs and limited access to high-paying jobs contribute to LGBT poverty. Many studies show that raising the wages of low-wage workers through an increase in the minimum wage can reduce poverty in the United States. In this report, we assess the contribution of low-wage jobs to LGBT poverty and to the LGBT poverty gap by simulating the impact of an increase in the federal minimum wage to $10.10 per hour (up from the current $7.25 federal minimum wage) on the family incomes of same-sex couples and different-sex couples.
Data on same-sex couples in the American Community Survey (ACS) is the only source that provides detailed data on hours and income and a large enough sample to provide the necessary information for a simulation for some part of the LGBT community. Using the 2012 ACS, we find that the simulated higher minimum wage would reduce poverty rates for all couple-based families, including same-sex couples.
Key findings
- An increase in the minimum wage would reduce the poverty rate by 24% for different-sex couples, 25% for same-sex female couples, and by 30% for same-sex male and different-sex unmarried couples.
- Unmarried different-sex couples would see the biggest poverty reduction benefit from a higher minimum wage.
- At least 20,000 individuals in same-sex couples would be lifted out of poverty.
- The change would slightly narrow the gap in poverty rates by sexual orientation, but same-sex female couples and unmarried different-sex couples would remain more likely to be in poverty and same-sex male couples slightly less likely than different-sex married couples to be in poverty.
- Among same-sex couples, the people who would gain the most from the higher minimum wage are African Americans, couples with children, people with disabilities, people aged 18-24, those without high school degrees, and those living in a rural area. For example, among all people in same-sex couples, 6.6% of people are African American, but they are 13.6% of the group of people in same-sex couples who would move out of poverty. Similarly, same-sex couples with children make up 20% of all couples, but they are 37% of families leaving poverty.
- Poverty rates fall for the most vulnerable people in same-sex couples—particularly women and African Americans—as well as for children in households led by same-sex couples.
- The groups who gain the most among different-sex couples are similar to those in same-sex couples, but Hispanic different-sex couples and different-sex couples aged 25-34 also benefit tremendously (and proportionally more than same-sex couples) from the minimum wage increase.
Defining poverty
The U.S. Census Bureau uses data from surveys of households to calculate official poverty rates. The Census Bureau compares an individual’s or family’s income to the Federal Poverty Line (FPL), which is the income threshold. The FPL takes into account the number of children under 18 and the age of the householder, and varies according to family size. In 2012, the poverty line for a single person (under 65 years old) household was $11,945, for a two-person household (with no children) was $15,374, and for a four-person household was $23,681.
In this study, we use data from the 2012 American Community Survey (ACS), a nationally representative survey that collected data on more than 3 million individuals in 2012 via mail-in responses, CATI (computer-assisted telephone interview), and CAPI (computer-assisted personal interview).
The ACS allows us to identify people in same-sex relationships based on their household composition. The householder in each housing unit must define a relationship between him- or herself to everyone else in the household. We count a same-sex couple when the householder identifies another same-sex member of the household as his or her “unmarried partner.”
We adjusted the Census Bureau procedure to measure poverty within families so that unmarried partner couples, along with any children under 18 in their households, are also included as families. Otherwise, we follow the Census procedure for measuring poverty. A family is poor, for official statistical purposes and in this study, if their total family income is below the FPL for a family of that size. We calculate poverty rates by dividing the number of poor families by the total number of people.
An individual is poor if he or she lives in a family that has an income below the FPL. In some comparisons by personal characteristics, such as race and education level, we look more specifically at individuals who are in couples.
Simulating an increase in the minimum wage
We simulate an increase in the minimum wage to $10.10 per hour in two steps. First, we calculate poverty rates among couples with their reported earnings in the ACS. Then we replace the estimated hourly wage of people earning less than $10.10 per hour with the new minimum wage and recalculate poverty rates. We use the $10.10 per hour comparison because that is the federal minimum wage level that would be in force after two years if Congress enacts the Minimum Wage Fairness Act (S. 1737/ H.R. 1010).
The ACS data do not include a direct measure of hourly wages, unfortunately. Therefore, we first estimate each employed individual’s hourly wage by dividing their current earnings from employment by the total number of hours they worked over the last 12 months. We estimate the total number of hours worked by multiplying the weeks worked over the last 12 months, measured as the midpoint of the reported interval of weeks worked (for example, the midpoint of 47 to 50 weeks is 48.5), times the number of hours that the respondent reports usually working per week.
For anyone whose estimated wage is less than $10.10 per hour, we raise their wage to $10.10 and multiply it by the same hours worked over the last 12 months to get their simulated income. We then use that new income to recalculate the poverty rates.
Perhaps the most important assumption in this procedure is that there will be no change in hours worked by individuals as their wage changes, so full-time and part-time workers earn the new wage for the same hours that they actually worked in that year. In other words, we assume that there are no employment effects of an increase in the minimum wage. While there is an academic and policy debate about the impact of a higher minimum wage on changes in employment, many economists see the weight of the evidence as supporting a prediction of little to no impact on employment.
Some other assumptions will tend to make workers’ simulated earnings somewhat higher than might be actually expected. First, we do not distinguish low-wage workers who receive tip income and therefore are eligible for a lower cash minimum wage. Under S. 1737, tipped workers’ minimum cash wage would start at $3.00 (up from its current level of $2.13 per hour) and then rise each year until it reaches 70% of the minimum wage at that time. Also, we are not able to identify which workers might be exempt from the minimum wage, either because of the type of work or their employer’s size.
However, there are other reasons that our estimates might underestimate the impact of a minimum wage increase. First, we also do not take into account any rise in state minimum wage rates above $10.10 per hour. Second, we do not take into account any “spillover” effects that would raise the wage rates of people currently earning more than the minimum wage. For these and other reasons, existing research suggests that these types of simulations will underestimate the true impact of a higher minimum wage on poverty. Therefore our estimate of same-sex couples moving out of poverty is a conservative one.
Poverty rates fall with a higher minimum wage
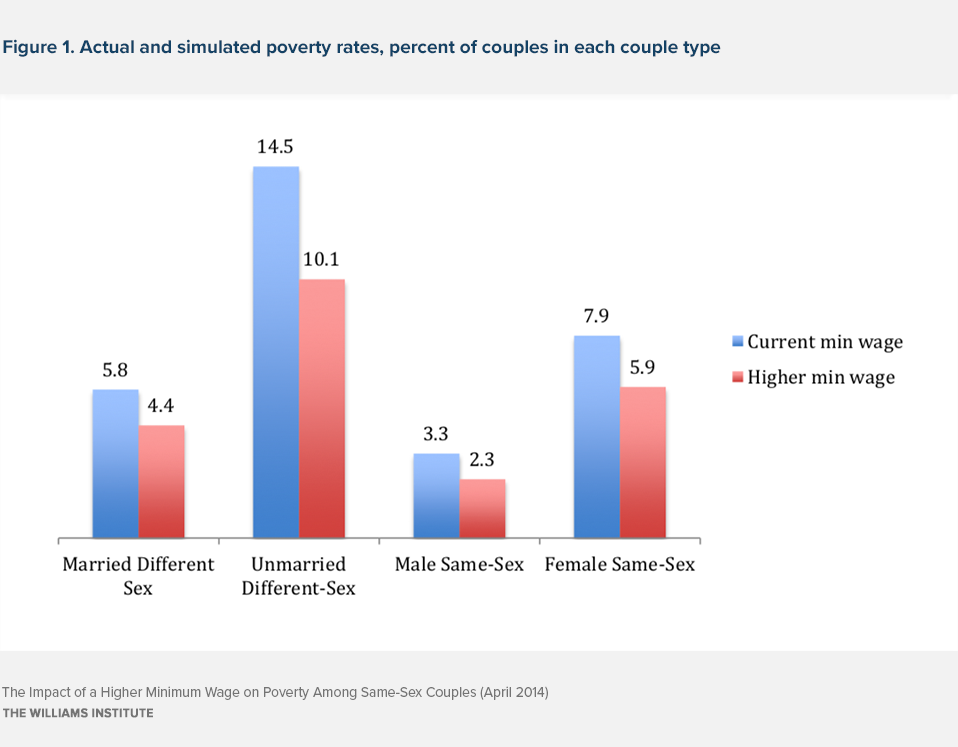
To start, Figure 1 shows that with the current minimum wage, same-sex male couples have the lowest poverty rate of 3.3%, followed by married different-sex couples at 5.8%. Female same-sex couples have a higher poverty rate of 7.9%, and unmarried different-sex couples have by far the highest poverty rate, 14.5%.
Our simulation shows that raising the minimum wage to $10.10 per hour would reduce poverty by 24% or more for each group of couples. Figure 1 also shows the simulated poverty rates for the four couple types. Married different-sex couples’ 2012 poverty rate falls from 5.8% to 4.4% with the minimum wage boost. Unmarried different-sex couples show the biggest drop, from 14.5% to 10.1%, a 30% drop. Male same-sex couples had the lowest poverty rates, but even theirs dropped from 3.3% to 2.3%. Female same-sex couples had poverty rates higher than either married or male couples, and their poverty rate fell from 7.9% to 5.9%, a drop of 24%.
Poverty gaps change relatively little
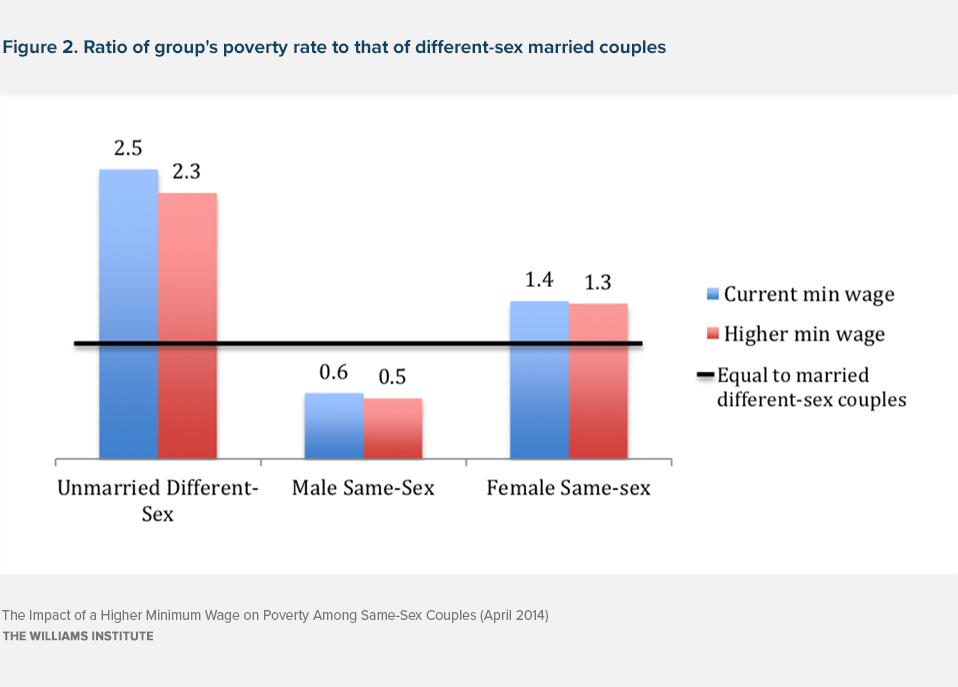
A higher minimum wage leads to some reduction in the poverty gaps for the two groups more likely to be poor than married different-sex couples: female same-sex couples and unmarried different-sex couples. There are two ways to assess the change in the poverty gap: changes in the actual differences in poverty rates or changes in ratios between the groups. Both measures show fairly small changes in the gaps between groups of couples.
If we look at the difference in poverty rates, which is 2.1 percentage points (equal to 7.9 – 5.8) for female vs. married couples, the convergence in the poverty rates between same-sex female and different-sex married couples appears a bit larger: the minimum wage increase would lead to a fall in the difference to 1.5 percentage points (equal to 5.9 – 4.4). The convergence in poverty rates across couple types also looks larger when we compare same-sex female to unmarried different-sex couples: there the difference in poverty rates falls from 8.7 percentage points to 5.7 percentage points.
However, the changes in the ratios provide the better measure of the relative probability of being poor between groups. Figure 2 shows that an increase in the minimum wage leads to a slight decrease in the ratio of female same-sex couples’ poverty rate to married couples’ poverty rate, from 1.4 (equal to 7.9/5.8) to 1.3 (equal to 5.9/4.4). The ratio drops from 2.5 to 2.3 for unmarried different-sex couples. The similarity in ratios before and after the simulation shows that the poverty rates for each group are changing in very similar proportions.
For male same-sex couples, the poverty gap actually favors the male couples, since they have a lower poverty rate than different-sex couples. Depending on how the gap is measured, raising the minimum wage has different effects. The absolute difference in poverty rates between same-sex male and different-sex married couples falls (from 5.8-3.3=2.5 percentage points to 4.4-2.3=1.1 percentage points), suggesting that the change in the minimum wage would lead to a smaller positive poverty gap for same-sex male couples’ compared to married couples. However, the relative poverty rates, given by the ratio of the rates across couple types, falls after increasing the minimum wage (from 3.3/5.8=0.6 to 2.3/4.4=0.5), indicating that the poverty rate for male same-sex couples would move farther away from married couples’ poverty rate. Thus, there is a larger relative impact of a minimum wage increase for same-sex male couples than for different-sex married couples.
Since poverty rates vary along many different individual and household characteristics, we would like to know whether sexual orientation plays an independent role in predicting poverty for an individual before and after a minimum wage increase. We use a statistical technique that allows us to focus on the sexual orientation effect by holding the education level, employment, age, race, ethnicity, fluency in English, and disability of both members of the couple constant, as well as the state and metropolitan status where the couple resides, and the number of children and number of adults in the household. In other words, instead of comparing the whole group of same-sex couples with the whole group of married different-sex couples, we compare couples from each of these groups with the same characteristics. Thus, we isolate the effect of sexual orientation on the probability of being poor.
The results of that procedure show that the families of same-sex female couples are significantly more likely to be in poverty than different-sex married-couple families with similar characteristics, both before and after the simulated minimum wage increase. Households led by a female same-sex couple are 2.9 percentage points more likely to be in poverty than their different-sex married household counterparts, after accounting for other factors that contribute to poverty listed in the previous paragraph. Increasing the minimum wage lowers that effect to 2.3 percentage points, although the difference is not statistically significant. While the overall poverty rate is lower for gay male couples than for married couples, the detailed comparisons show that same-sex male couple households are neither more nor less likely to be poor, either before or after the simulation.
The biggest gains of an increase in the minimum wage go to people in different-sex unmarried couple households. With the current minimum wage, they are 2.6 percentage points more likely than those in different-sex married couples to be in poverty, holding other characteristics constant. With the higher minimum wage, they are only 1.7 percentage points more likely than different-sex married couples to be poor.
We can use the changes in poverty rates to estimate the actual number of families moving out of poverty. Here we draw on counts of same-sex couples from the 2010 U.S. Census, which the Census Bureau corrected to undo errors in responses to the sex question that is used to identify same-sex couples. After making the corrections, the Census Bureau counted 646,464 same-sex couples, 313,577 of whom were male couples, and 332,887 of whom were female. We use the Census 2010 counts instead of estimates of the number of same-sex couples from the ACS because of those detailed corrections. We use the 2012 ACS percentages of same-sex couples in poverty because they are the most up-to-date.
As shown in Figure 1, the poverty rate for male same-sex couples falls by one percentage point, accounting for approximately 3,100 couples. The poverty rate for female same-sex couples falls by two percentage points or 6,600 couples. In total, almost 10,000 same-sex couples, or 20,000 individuals, leave poverty as the result of the simulated increase in the minimum wage.
Characteristics of same-sex couples moving out of poverty
Using the 2012 ACS data, we can see exactly which people in same-sex couples would move out of poverty given an increase in the minimum wage. We see that some groups of same-sex couples would benefit more from an increase in the minimum wage than would others by comparing a group’s share of all same-sex couples to their share of the poverty leavers. Several groups gain disproportionately:
- African Americans in same-sex couples: Among all same-sex couples, 6.6% of people in same-sex couples are African American, but they are 13.6% of the group of people in same-sex couples who would move out of poverty.
- Couples with children: Same-sex couples with children make up 20% of all couples, but they are 37% of families leaving poverty.
- People with disabilities: In same-sex couples, 11% of individuals report a disability, but people with disabilities are 25% of people leaving poverty.
- Young people in same-sex couples: People who are age 18-24 are 6.5% of all same-sex couples but 26.1% of poverty leavers.
- People without a high school degree: People in same-sex couples who do not have a high school degree are 5.5% of same-sex couples but 14.6%of same-sex couples moving out of poverty. Overall, all people who do not have a bachelor’s degree are more likely to move out of poverty than are those with a bachelor’s or a higher degree.
- Those living in rural areas: Same-sex couples living in a rural area are 13.3%of all same-sex couples, but 28.7% of poverty leavers.
Focus on most vulnerable groups of families
In previous research, we identified particularly high poverty rates for African-American same-sex couples and children living in same-sex couples. The minimum wage increase simulation shows that poverty rates for those same-sex couples would fall with the higher minimum wage, although they would remain higher for same-sex couples than for different-sex married couples from the same groups.
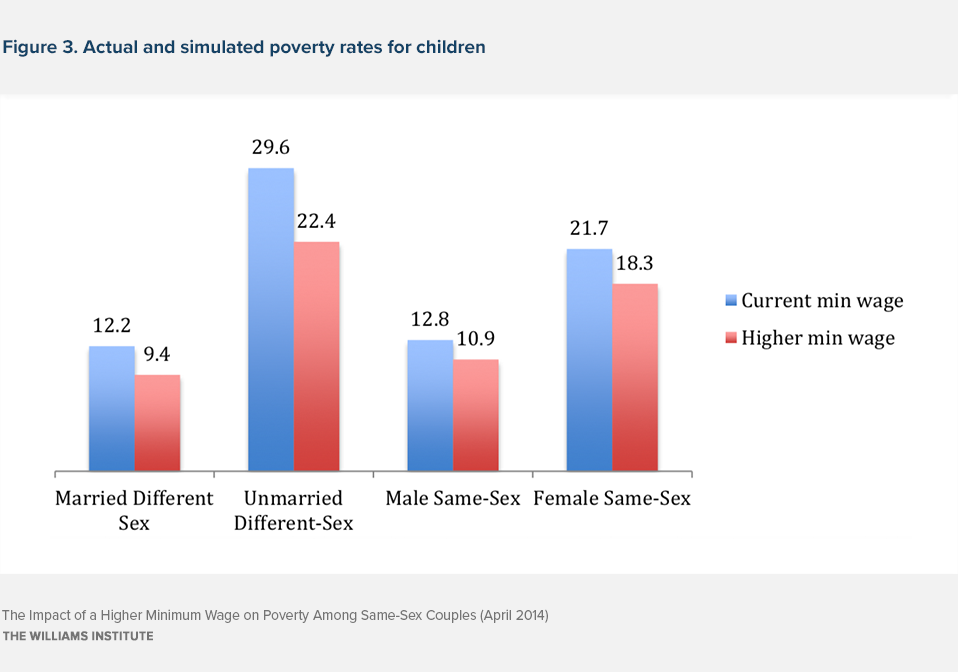
Figure 3 shows the poverty rates for children living with parents of different couple types. Children living with unmarried different-sex couples or with female same-sex couples show the biggest drops in poverty rates as a result of the higher minimum wage for their parents. Children living with male same-sex couples also see a drop, and they have slightly higher poverty rates than married different-sex couples.
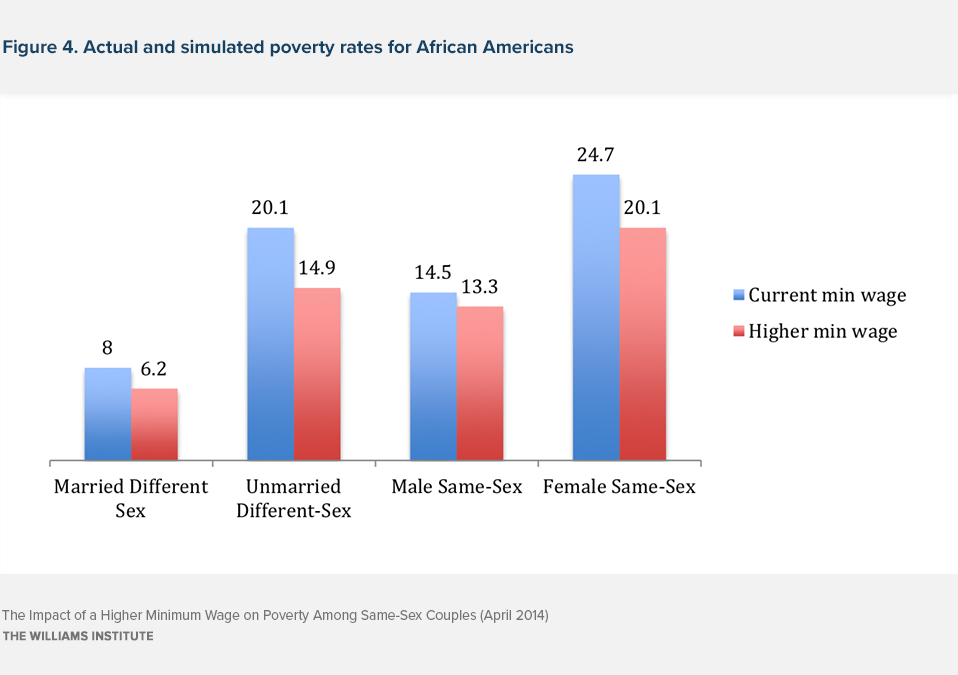
Figure 4 presents the same comparison for African Americans in the four couple types. Again, the minimum wage increase has the biggest benefit for African American women in same-sex couples, reducing their poverty rate from 24.7% to 20.1%, and for African Americans in different-sex unmarried couples, reducing their poverty rate from 20.1% to 14.9%. African American men in same-sex couples see a much smaller drop and have higher poverty rates than African American married people.
Conclusion
Overall, this simulation demonstrates that an increase in the minimum wage to $10.10 per hour would help many individuals and families–at least 20,000 people in same-sex couples would no longer be poor. The subgroups of the LGBT population who are most likely to be poor appear to benefit the most from a higher minimum wage, including African Americans, couples with children, people with disabilities, young people, and those living in rural areas. If there are spillover effects that raise wages for people now earning more than $10.10 per hour, then the gains could be even larger.
Unfortunately, other datasets that allow for measures of poverty and of sexual orientation for all individuals do not have sufficient data to do the same kind of simulation. In addition, we do not have the data to do any simulations for transgender people. But it seems very likely that the drop in poverty for same-sex couples would be seen for all LGBT people if the minimum wage were higher. The lack of equal opportunities for high-wage work and the likely disproportionate clustering of LGBT people in low-wage jobs means that a higher minimum wage would have benefits for all LGBT people.
Download the brief